Rumus Bangun Datar

1. Persegi

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun persegi, antara lain:

Rumus Luas persegi, yaitu:

L = S x S

Rumus Keliling persegi, yaitu:

K = S + S + S + S ataupun K = 4 x S

Keterangan:

• L: Luas
• K: Keliling
• S: Sisi

Contoh Soal:

Perhatikanlah gambar di bawah ini:

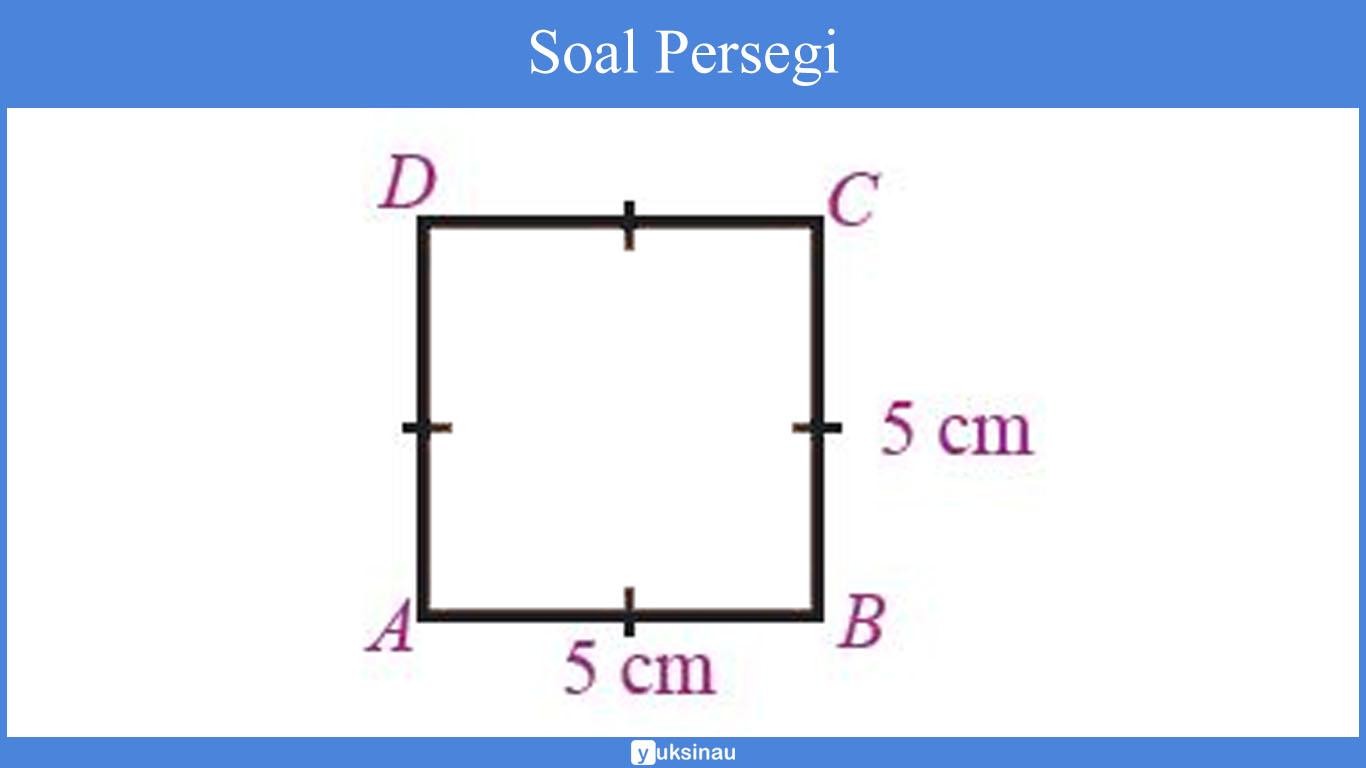
Dari gambar di atas, tentukan:

a. Tentukan luas perseginya:
b. Tentukan keliling perseginya:

Jawab:

a. Rumus Luas persegi ABCD yakni: s x s, sehingga

= 5 cm x 5 cm
= 25 cm2.

Jadi, luas persegi ABCD yaitu: 25 cm2.

b. Rumus Keliling persegi ABCD ialah: 4 x s, sehingga

= 4 x 5 cm
= 20 cm.

Jadi, jumlah keliling persegi ABCD tersebut yaitu 20 cm.

2. Persegi Panjang

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun persegi panjang, antara lain:

Rumus Luas persegi panjang, yaitu:

L = p x l

Rumus Keliling persegi panjang, yaitu:

K  = 2 x (p + l)

Keterangan:

• L: Luas
• K: Keliling
• p: panjang
• l: lebar

Contoh Soal 

Suatu bangun persegi panjang, mempunyai p = 10 cm dan l = 5 cm, terdiri atas  EFGH:

Pertanyaan:

a. Hitunglah luas persegi panjang EFGH:
b. Hitunglah keliling persegi panjang EFGH!:

Jawab:

a. Rumus luas persegi panjang EFGH adalah L= p x l, sehingga

L  = 10 cm x 5 cm
L = 50 cm2.

Jadi, luas persegi panjang EFGH yaitu 50 cm2.

b. Rumus Keliling sama persegi panjang EFGH adalah: 2 x (p + l), sehingga

= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm

Jadi, keliling persegi panjang EFGH yaitu 50 cm.

3. Segitiga

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun Segitiga, antara lain:

Rumus luas segitiga yaitu:

Luas = ½ x a x t

Rumus keliling segitiga yaitu:

Keliling = s + s + s atau K = a + b + c

Contoh Soal

Suatu bangun segitiga memiliki sebuah ukuran seperti yang tertera di gambar di bawah ini:

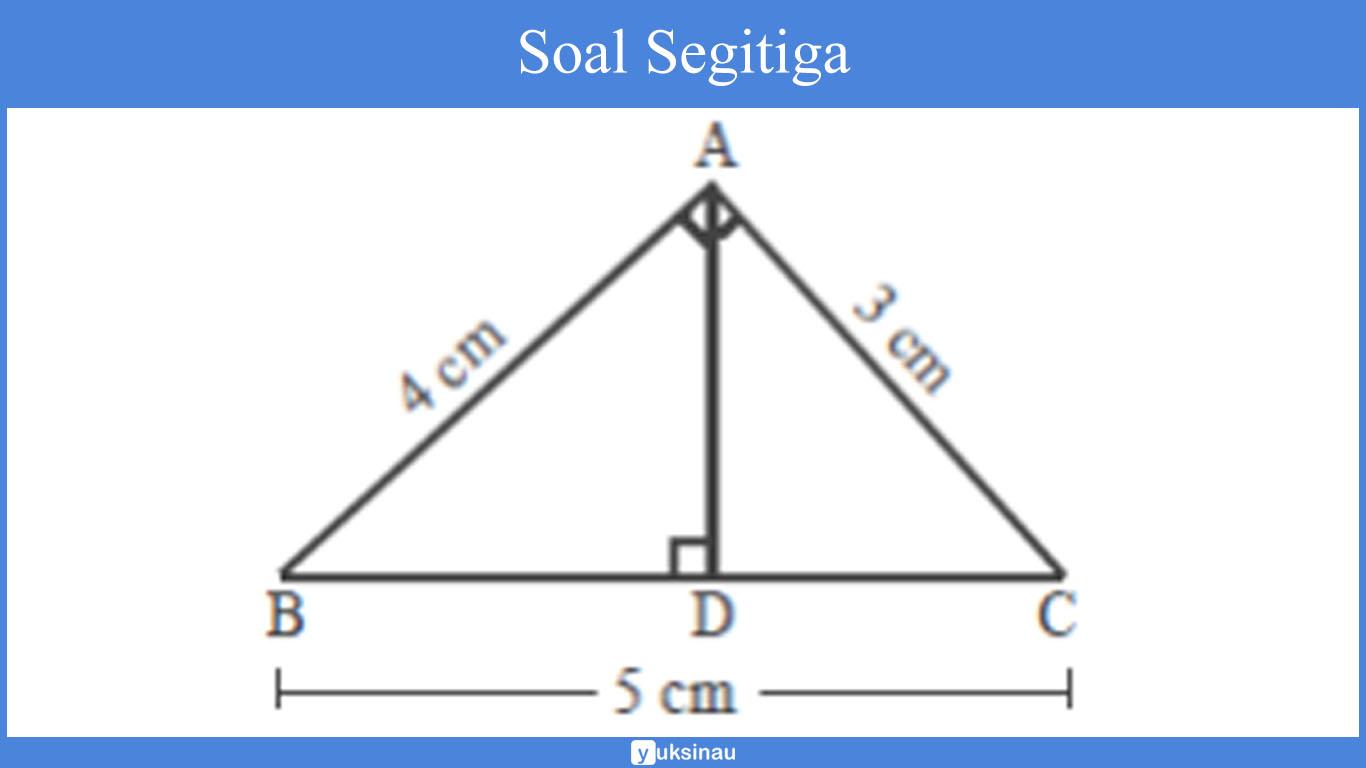
Pertanyaan:

a. Hitunglah luas segitiga :
b. Hitunglah keliling segitiga :

Jawab:

a. Luas segitiga Rumusnya yaitu ½  x  a  x  t, sehingga

= ½ x 3 cm x 4 cm

= ½ x 12 cm2.
= 6 cm2

Jadi, hasil perhitungan dari luas segitiga adalah 6 cm2.

b.  Keliling segitiga nya adalah = s + s + s, sehingga

= AC+AB+BC
= 3cm+4cm+5cm
= 12 cm.

Jadi, keliling segitiga adalah 12 cm.

4. Jajar genjang

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun Jajar agenjang, antara lain:

Nama	Rumus
Keliling (K)	K = 2 × (a + b)
Luas (L)	L = a × t
Sisi Alas (a)	a = (K ÷ 2) – b
Sisi Sisi Miring (b)	a = (K ÷ 2) – a
t diketahui L	t = L ÷ a
a diketahui L	a = L ÷ t

Contoh Soal

Perhatikanlah gambar jajaran genjang ABCD di bawah ini!

Panjang BC = DA = 8 cm.

Pertanyaan:

a. Hitunglah luas jajaran genjang ABCD, merupakan:
b. Hitunglah keliling jajaran genjang ABCD, merupakan:

Jawab:

a. Luas jajaran genjang ABCD adalah = a x t, sehingga

= 8 cm x 7 cm
= 56 cm2

Jadi, luas jajaran genjang ABCD yaitu 56 cm2.

b. Keliling jajaran genjang ABCD adalah s + s + s + s, maka:

K = AB + BC + CD + DA, yakni :
K = 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm.

Jadi, keliling jajaran genjang ABCD adalah 32 cm.

5. Trapesium

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun trapesium, antara lain:

Nama	Rumus
Luas (L)
Keliling (K)	K = AB + BC + CD + DA
Tinggi (t)
Sisi a (CD)	atau CD = K – AB – BC – AD
Sisi b (AB)	atau AB = K – CD – BC – AD
Sisi AD	AD = K – CD – BC – AB
Sisi BC	BC = K – CD – AD – AB

Contoh soal:

Perhatikanlah bangun datar trapesium EFGH di bawah ini!

Panjang EH = FG ialah 8 cm.

Pertanyaan:

a. Tentukanlah luas trapesium EFGH:
b. Tentukanlah keliling trapesium EFGH:

Jawab:

a. Luas trapesium EFGH adalah:  ½ x (a + b) x t maka,

= ½  x  (16cm  +  6 cm) x  7 cm
= ½  x  22  cm x  7 cm
= 11cm  x   7 cm
= 77 cm2

Jadi, luas trapesium EFGH di atas adalah 77 cm2.

b. Keliling trapesium EFGH memiliki rumus yaknni: s + s + s + s, maka:

K = EF  +  FG  +  GH  +  HE
K = 16 cm  +  8 cm  +  6 cm  +  8 cm
= 38 cm.

Jadi, luas keliling trapesium EFGH di atas adalah 38 cm.

6. Layang – layang

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun Layang-Layang, antara lain:

Nama	Rumus
Luas (L)	L = ½ × d1 × d2
Keliling (K)	K = a + b + c + d
	K = 2 × (a + c)
Diagonal 1 (d1)	d1 = 2 × L ÷ d2
Diagonal 2 (d2)	d2 = 2 × L ÷ d1
a atau b	a = (½ × K) – c
c atau d	c = (½ × K) – a

Contoh Soal

Perhatikan layang layang ABCD di bawah ini!

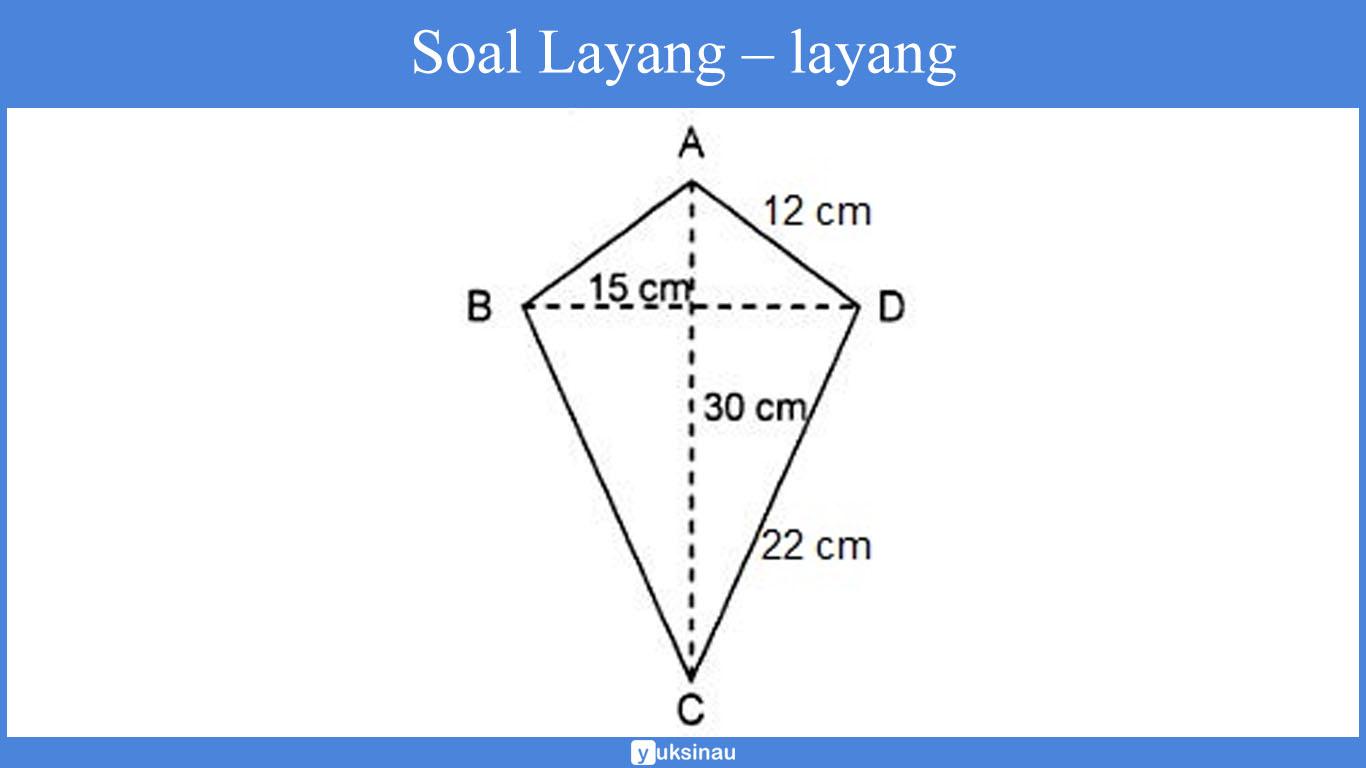
DiketahuI;

Panjang BC = panjang CD
Panjang AB = panjang AD

Pertanyaan:

a. Hitunglah luas layang layang ABCD!
b. Hitunglah keliling layang layang ABCD!

Jawab:

a. Luas layang-layang ABCD adalah = ½ x d1 x d2, sehingga

= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2

Jadi, luas layang layang ABCD tersebut yaitu 225 cm2.

b. Keliling dari layang-layang ABCD adalah: 2 x (x + y), sehingga

= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm

Jadi, keliling layang layang ABCD yaitu 68 cm.

7. Belah Ketupat

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun Belah ketupat, antara lain:

Nama	Rumus
Keliling (K)	K = s + s + s + s
	K = s × 4
Luas (L)	L = ½ × d1 × d2
Sisi (s)	s = K ÷ 4
Diagonal 1 (d1)	d1 = 2 × L ÷ d2
Diagonal 2 (d2)	d2 = 2 × L ÷ d1

Contoh Soal:

Perhatikan belah ketupat di bawah ini!

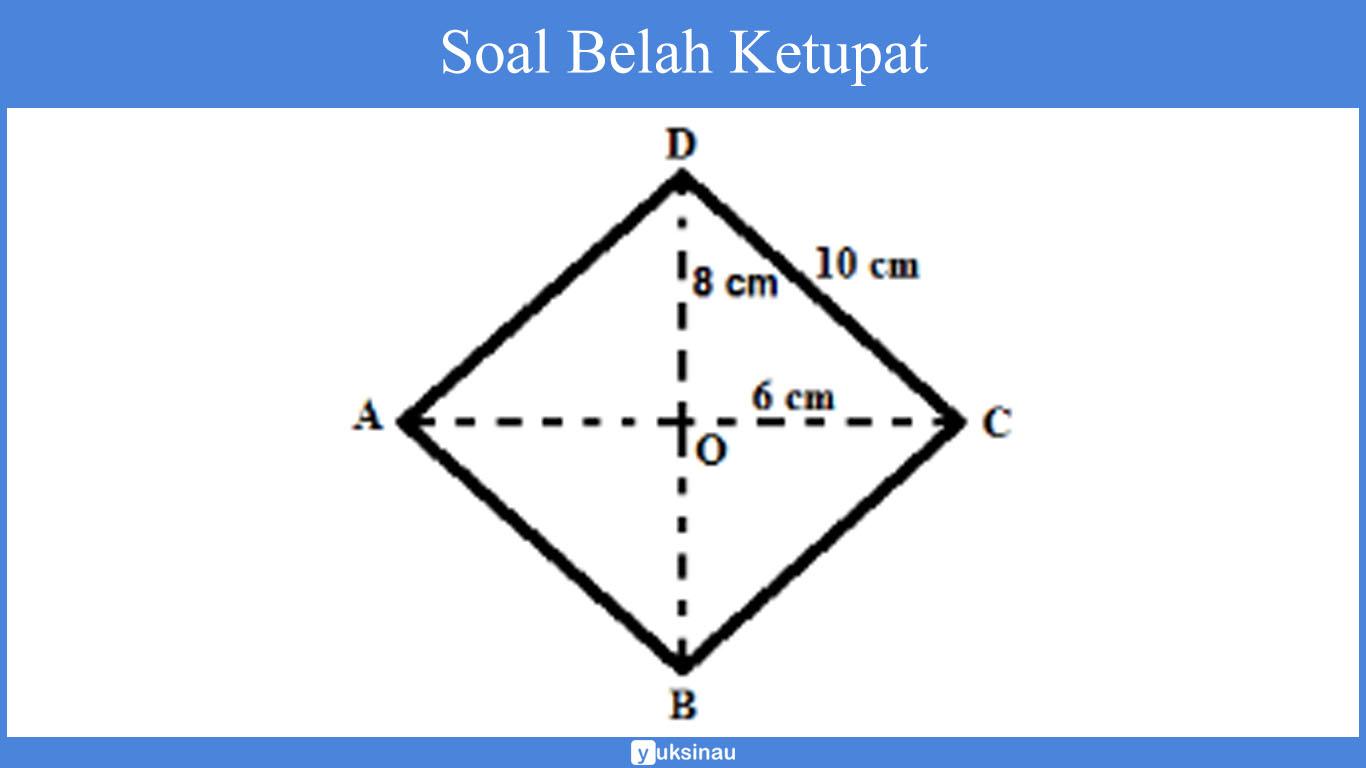
Panjang AC adalah 12 cm
Panjang BD adalah 16 cm

Pertanyaannya yaitu:

a. Tentukanlah luas belah ketupat ABCD!
b. Tentukan simak keliling belah ketupat ABCD!

Jawab:

a. Luas belah ketupat ABCD adalah = ½ x d1 x d2, sehingga
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2

Jadi, luas belah ketupat ABCD yaitu 96 cm2.

b. Keliling belah ketupat ABCD adalah: s + s + s + s, sehingga
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm

Jadi, keliling belah ketupat ABCD yaitu 40 cm.

8. Lingkaran

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun Lingkaran, antara lain:

• phi (π): 3,14159 (dibulatkan menjadi 3,14) atau 22/7. 

Nama	Rumus
Diameter (d)	d = 2 × r
Jari-jari (r)	r = d ÷ 2
Luas (L)	L = π x r x r atau L = π x r2
Keliling (K)	K = π x d
Mencari r	r = K/ 2π
	r = √L/ √π

Contoh Soal

Mencari Luas

Apabila diketahui suatu lingkaran memiliki diameter 14 cm. Berapakah luas lingkaran tersebut?

Jawab:

Diketahui:

• d = 14 cm

Sebab d = 2 × r maka:
r = d/2
r = 14/2
r = 7 cm

Ditanyakan:

• Luas lingkaran?

Penyelesaian:

Luas = π × r²
Luas = 22/7 × 7²
Luas = 154 cm²

Sehingga, luas lingkaran tersebut yaitu 154 cm².

Mencari Keliling

Hitunglah keliling lingkaran yang memiliki jari-jari 20 cm.

Jawab

Diketahui:

• r = 20 cm
• π = 3,14

Ditanyakan:

• Keliling lingkaran?

Jawab:

Keliling = 2 × π × r
K            = 2 × 3,14 × 20
K            = 125,6 cm

Sehingga, keliling lingkaran tersebut yaitu 125,6 cm.

Mencari Diameter

Diketahui suatu lingkaran mempunyai keliling sebesar 66 cm. Tentukan berapa diameter lingkaran tersebut!

Jawab

Diketahui:

• Keliling = 66 cm

Ditanyakan:

• Diameter lingkaran?

Jawab:

Keliling = π × d

Dalam mencari diameter, maka kita akan menggunakan rumus mencari diameter, yaitu:

Rumus mencari diamter ialah d = keliling / π

• d = 66 / (22/7)
• d = (66 × 7) / 22
• d = 21 cm

Sehingga, diameter lingkaran tersebut yaitu 21 cm.

Sekian, Semoga Bermanfaat !!!